Generate Content¶
Perché usare la generazione procedurale?
I primi videogiochi la usavano per ridurre la dimensione del gioco: creando le textures e i livelli in tempo reale, non era necessario memorizzarle nella cartuccia, ad esempio.
Questo ha permesso di creare giochi che andassero oltre i limiti fisici imposti dalla tecnologia del momento. (vedi Elite)
NB: non tutti i metodi di generazione si basano sull'Intelligenza Artificiale
In questo sito c'è un elenco dei videogiochi e dei metodi di Generazione che usano: http://pcg.wikidot.com/
Procedural Content Generation (PCG)¶
cosa si può generare?
NPC behavior¶
Quest / Narrativa¶
Vedi The Sims
Audio¶
Visual¶
- ottimizzazione textures
- rimozione dei rumori
- miglioramento qualità video
- hyper-motion
Modelli¶
vedi No Man's Sky No man's sky
Livelli / Mappe / Percorsi¶
- creazione procedurale di contenuti
- generare nuovi ambienti / environment
- creare nuovi assets
- valutare la difficoltà
Esempi: - Civilization - AI Dungeon https://play.aidungeon.io
Items / Weapons¶
Game mechanics / Rules¶
Reward schedules¶
Vantaggi¶
- ridurre costi di sviluppo creando automaticamente contenuti sulle regole dei designers?
- possiamo costruire mondi che si adattano ai gusti del giocatore?
- possiamo creare giochi infiniti?
- possono i computer creare nuove forme di gioco e di creatività?
Limiti¶
- Speed Real-time o design-time?
- Reliability Catastrophic failures break gameplay
- Controllability Allow specification of constraints and goals
- Diversity Content looks like variations on a theme
- Creativity Content looks "computer-generated"
Metodi di generazione¶
Tiles-based approach¶
Search-Based¶
- A search algorithm
- A content representation
- evaluation functions
Solver-based¶
Ropossum https://www.youtube.com/watch?v=FM3v0tbdKrs
Metodi Frattali¶
Gli approcci frattali prendono il nome dai famosi oggetti matematici poiché hanno alcune proprietà simili. Questi approcci di generazione procedurale si basano su sistemi di strati successivi a scale diverse, un po' come i frattali. Vedremo due tipi di approcci frattali: metodi Grammar-based e Noize Based
Grammar-based¶
o production rules, regole di produzione.
Una grammatica formale può essere definita come un insieme di regole che si applicano ad un testo. Le regole grammaticali permettono di trasformare una sequenza di caratteri (stringa) in un'altra. Ad esempio queste due regole:
A -> AB
B -> A
A si deve trasformare in AB. La seconda che ogni lettara B si deve trasformare in A. Ci sono molti modi di applicare le grammatiche formale in AI, e il Sistemi-L sono uno di essi.
L-System / Sistemi-L¶
Gli L-Systems sono molto usati per la generazione di piante e vegetali. Hanno regole ricorsive, che permettono di creare facilmente forme frattali. In natura molte piante hanno forme frattali, ad esempio questo cavolo:
Un L-System è definito da un alfabeto, da un inseme di regole, da modifiche e da un assioma di partenza (il carattere che consideriamo il punto di partenza).
Ad esempio se abbiamo come alfabeto solo le lettere A e B: {A,B} e le due regole di prima:
A -> AB
B -> A
A e applichiamo più volte le regole ai risultati precedenti (con n che identifica il numero di volte che la regola è stata applicata, è lo step di avanzamento), ottemiamo questo risultato:
n = 0 -> A
n = 1 -> AB
n = 2 -> ABA
n = 3 -> ABAAB
n = 4 -> ABAABABA
n = 5 -> ABAABABAAB
n = 6 -> ABAABABAABABAABABA
n = 7 -> ABAABABAABAABABAABABAABAABAABAAB
Ci si potrebbe chiedere dove sia il collegamento tra queste sequenze di caratteri e le piante. L'idea è di associare a ciascuna lettera una determinata azione di disegno grafico, così che una sequenza sia la rappresentazioen di uan serie di istruzioni.
Ad esempio consideriamo queste istruzioni:
F avanza di tot disegnando una linea
f avanza di tot senza disegnare
+ ruota n° a sinistra
– ruota n° a destra
[ tieni traccia della posizione e rotazione corrente
] ripristano la posizione e rotazione memorizzata
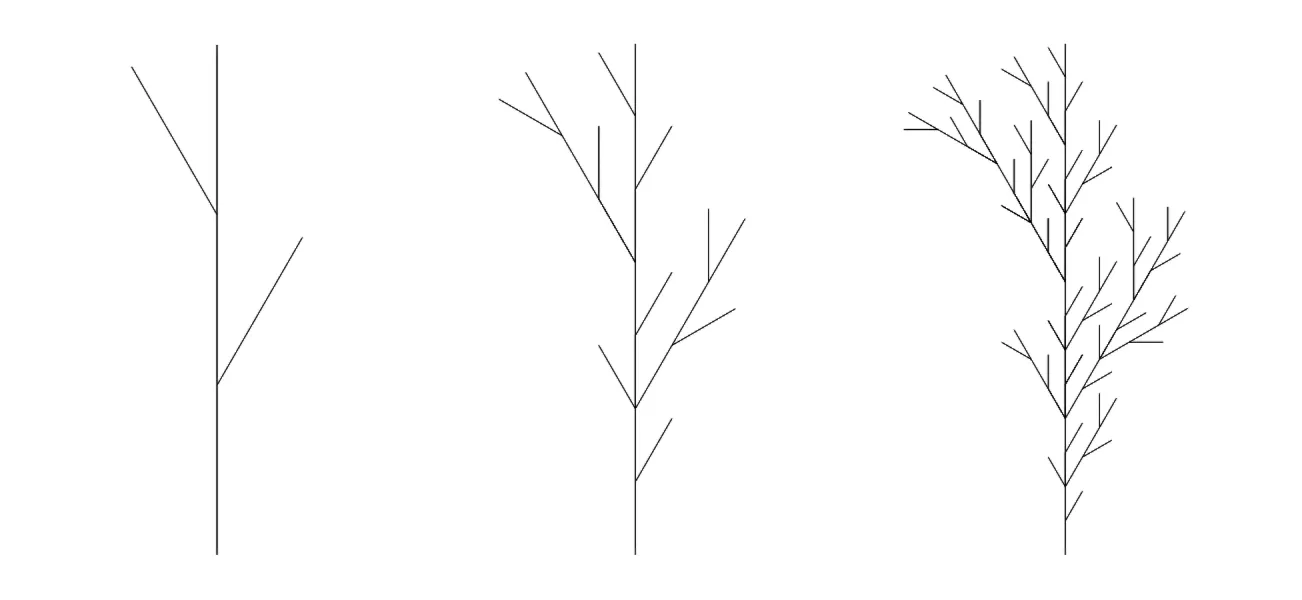
Regola grammaticale: F = F[-F]F[+F][F]
Assioma: F
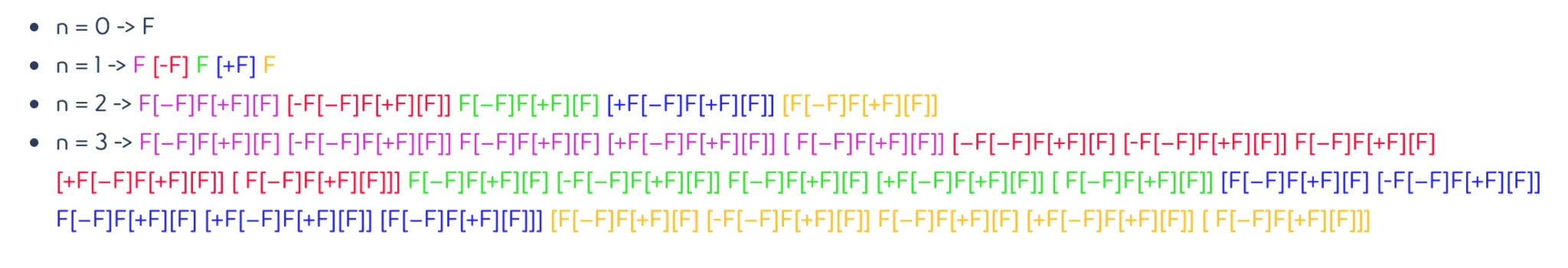
che rappresentati graficamente diventano:
che poi possono diventare
Altro esempio:
F disegna una line di una certa lunghezza (ad esempio 10 pixels)
+ ruota 90° a sinistra
– ruota 90 a destra
: tieni traccia della posizione e rotazione corrente
[ ] ripristano la posizione e rotazione memorizzata
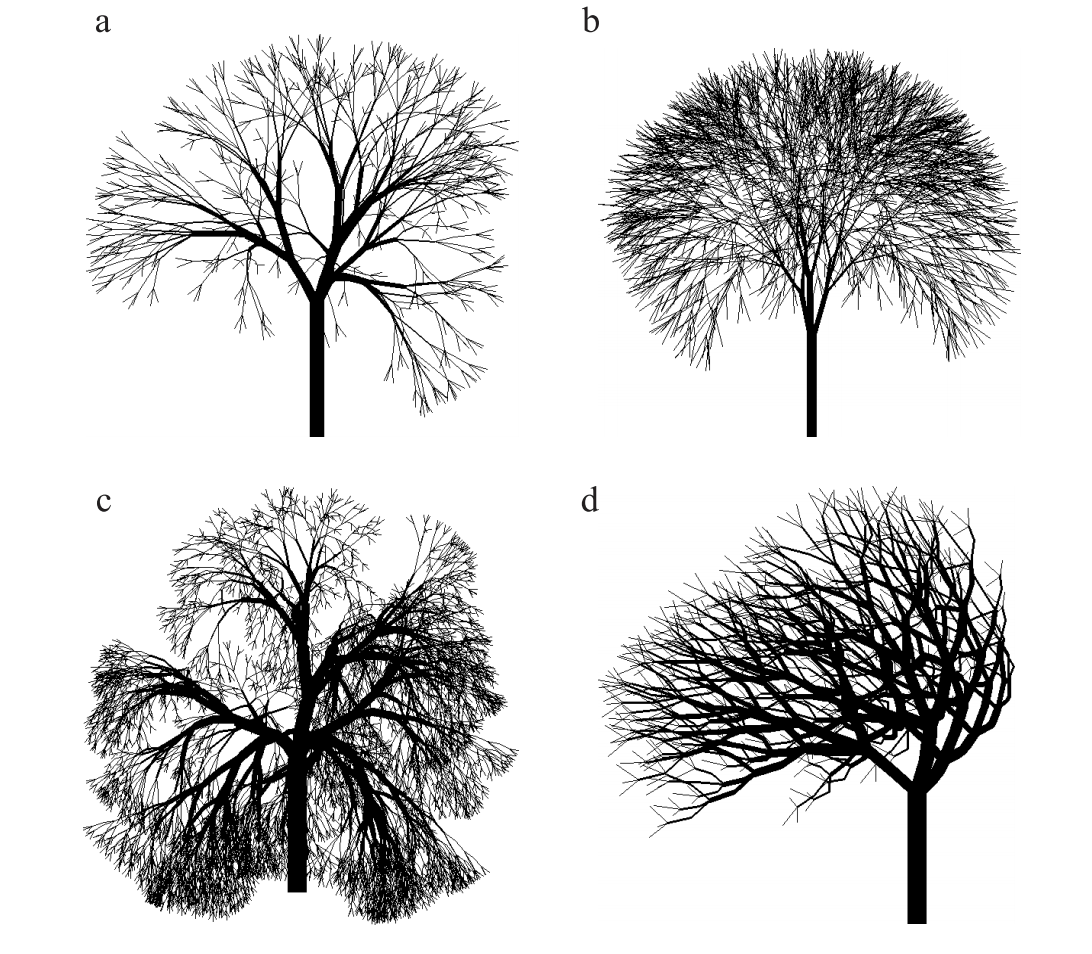
Regola grammaticale: F = F+F-F-FF+F+F-F
Assioma: F+F+F+F
Ci sono poi molte elaborazioni e utilizzi di questi sistemi per generare labirinti, stanze, rocce, etc...
Provate a giocare un po con questi Sistemi-L online: - vedere molti esempi animati: https://elc.github.io/posts/plotting-fractals-step-by-step-with-python/ - creare online http://www.kevs3d.co.uk/dev/lsystems/ - https://onlinemathtools.com/l-system-generator - L-SYSTEMS GENERATOR** is a 2D/3D modeling tool http://www.digitalpoiesis.org
vedi laboratorio L-Systems - http://www.malsys.cz/Process
Esempi: - generazione di un dungeon
Noize Based¶
Proviamo a disegnare un territorio realistico basandosi su una sequenza di numeri casuali.
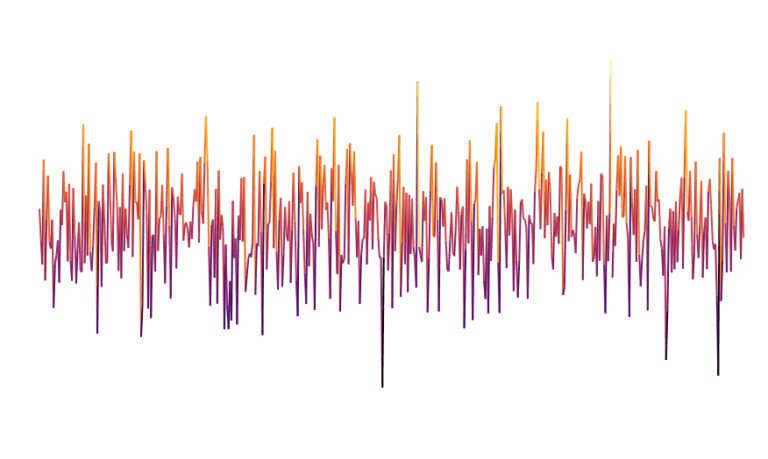
Quando scegliamo valori veramente casuali, abbiamo il Rumore bianco
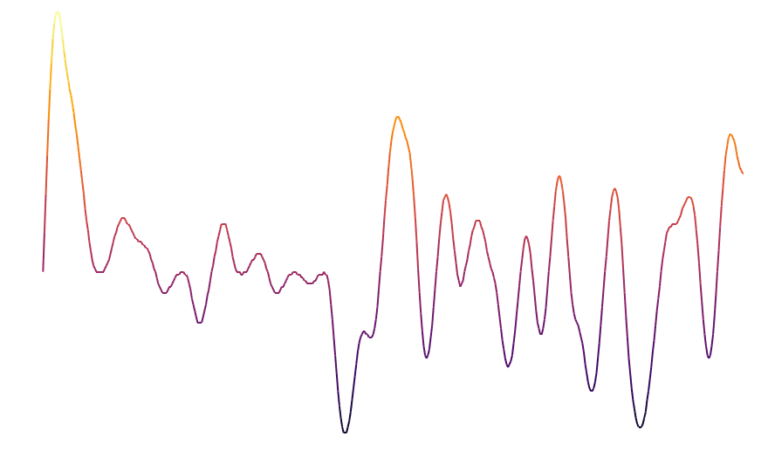
Ma se scegliamo dei generatori di casualità che mantenga delle caratteristiche "locali", dove ogni punto ha dei collegamenti con quelli adiacenti, abbiamo la Perlin noise, che garantisce delle curve localmente più morbide.
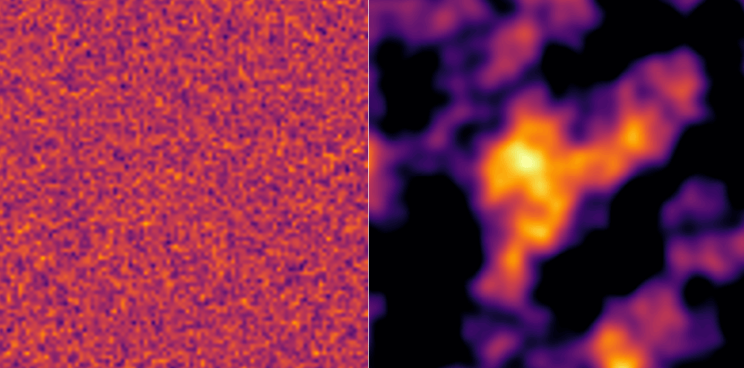
Se passiamo da una a due dimensioni, e riempiamo una superficie di rumore, ecco due esempi: rumore bianco a sinistra, Perlin a destra:
Usando l'intensità come elementi di altezza, possiamo costruire una superficie in 3D:
Il problema della Perlin è che tende a ripetere elementi con le stesse altezze. Possiamo risolvere usando diversi livelli, diversi strati di Perlin Noize a diverse ottave, uno macroscopico e poi sempre più dettagliate.
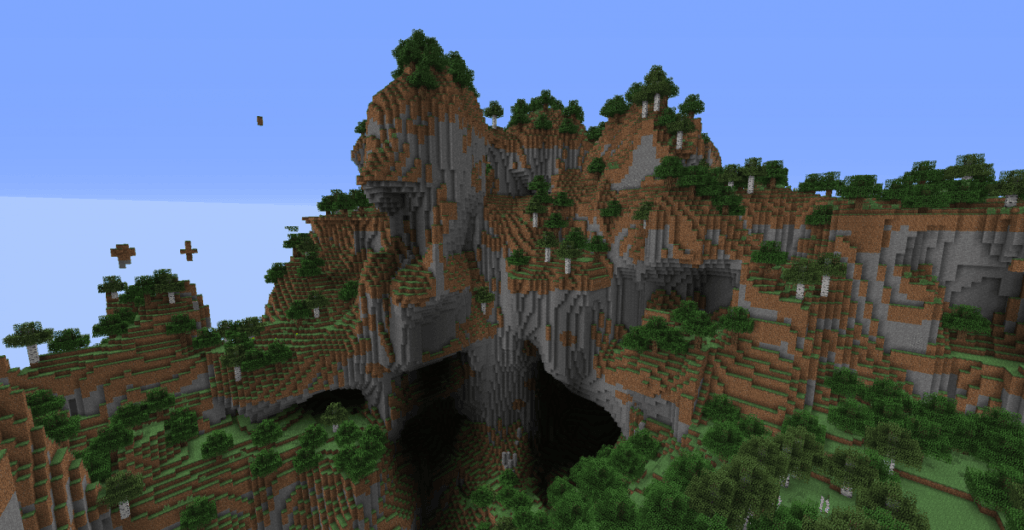
La Perlin è usata molto in Minecraft ad esempio. No man’s sky usa una variazione delle Perlin, la "Uber noise" che combina diversi tipi di Noize.
Cellular automata¶
Le cellular automata (CA) sono una classe di modelli matematici utilizzati per studiare il comportamento di sistemi complessi. Esse sono costituite da una griglia di celle, ognuna delle quali può assumere uno stato discreto (ad esempio "0" o "1"). Ogni cella si evolve nel tempo in base a regole predefinite, che dipendono dallo stato attuale della cella e dallo stato delle celle adiacenti.
Le CA possono essere utilizzate per simulare una vasta gamma di fenomeni naturali, come la diffusione del calore o la crescita di una colonia di batteri. Un esempio di CA famoso è la "Conway's Game of Life", un gioco creato da John Horton Conway nel 1970. In questo gioco, le celle assumono uno stato "vivo" o "morto" in base alle regole del gioco, che stabiliscono se una cella "viva" deve continuare a vivere o morire, e se una cella "morta" deve nascere o rimanere morta, in base al numero di celle adiacenti "vive" o "morte".
Esempio:
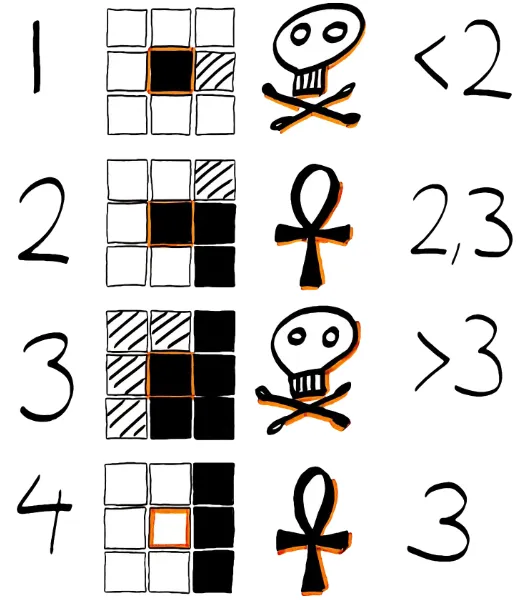
- cella viva con meno di due celle vive adiacenti muore (solitudine)
- cella viva con due o tre celle vive adiacenti sopravvive
- cella viva con più di tre celle vive adiacenti muore (sovrappopolazione)
- cella morta con esattamente tre celle vive adiacenti diventa una cella viva (riproduzione)
Gli effetti possono essere anche belle animazioni: 
Gli oggetti nel gioco della vita mostrano generalmente comportamenti che assomigliano a quelli che si trovano in natura poiché la loro evoluzione si basa su regole semplici. I Cellular Automata sono stati quindi ampiamente utilizzati per modellare ambienti e nei videogiochi per modellare pioggia, fuoco, flussi di fluidi o esplosioni. Sono stati utilizzati anche per la generazione di mappe o terreni.
Ad esempio, in un giovo dove il territorio è costituito da celle che posono essere o vuote o roccia.
L'automa cellulare è definito da un'unica regola di evoluzione:
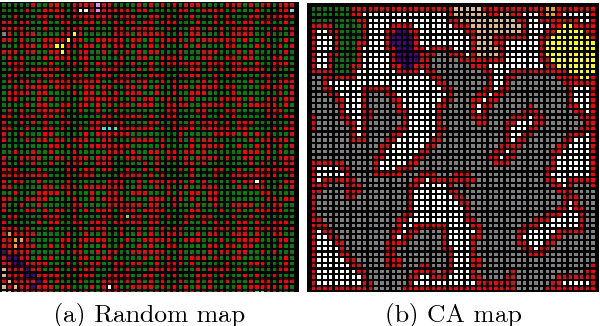
Una cella diventa o rimane di tipo roccia se almeno 5 delle sue vicine sono di tipo roccia, altrimenti diventa o rimane vuota.
Lo stato iniziale viene creato in modo casuale, ogni cella ha una probabilità del 50% di trovarsi in uno dei due stati.
PLAY - Conway's Game of Life - PLAY ONLINE - Generate Random Cave Levels Using Cellular Automata
Machine learning¶
GAN (Generative Adversial Networks)¶
Semantic Image Synthesis with Spatially-Adaptive Normalization https://nvlabs.github.io/SPADE/ video https://www.youtube.com/watch?v=p5U4NgVGAwg
https://www.theverge.com/2019/3/6/18222203/video-game-ai-future-procedural-generation-deep-learning
Utilizzo delle AI¶
There's an AI for That
Sito in continuo aggiornamento di servizi che usano le A.I. https://theresanaiforthat.com/
Generare Immagini¶
DALL·E
Creating Images from Text https://openai.com/blog/dall-e/
video: https://www.youtube.com/watch?v=C7D5EzkhT6A
Midjourney
https://www.midjourney.com
Stable Diffusion https://stability.ai
e il suo DreamStudio https://beta.dreamstudio.ai/
Muse
Gen 2023 https://muse-model.github.io/
Generare Testo¶
GPT3
OpenAI’s new GPT-3 language explained in under 3 minutes https://thenextweb.com/neural/2020/07/23/openais-new-gpt-3-language-explained-in-under-3-minutes-syndication/
Generare Labirinti¶
Approfondimenti¶
Videos: - Invisible cities https://www.youtube.com/watch?v=c3ewUbFqIuo - Electric Sheep https://www.youtube.com/watch?v=Va1KBtI81TY - Unity Art Engine https://unity.com/products/unity-artengine
Corsi: - Procedural Content Generation https://canvas.ucsc.edu/courses/7638